Exponential Growth
Exponential growth is characterized by an ever increasing growth rate or rate of decline. It eventually starts moving very quickly but remains a function of time. In other words, it doesn't suddenly jump to infinity. For example, exponential growth can be seen in the growth of bacteria, economies and certain environmental pollutants.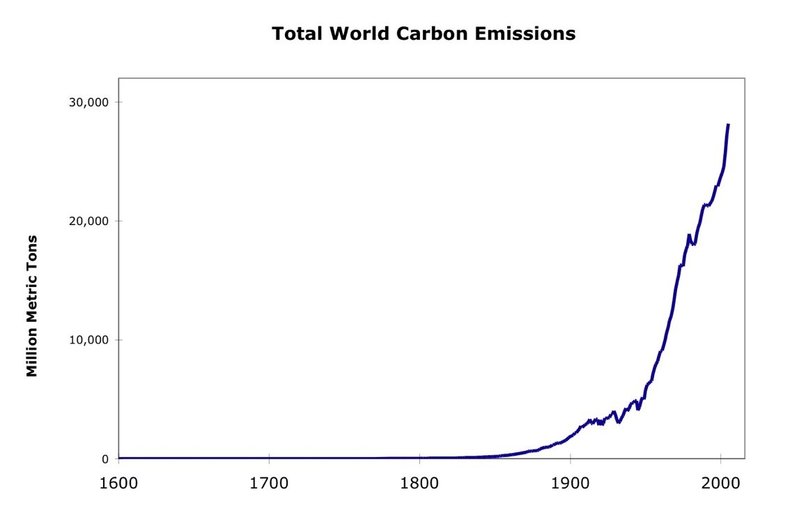
Hyperbolic Growth
Hyperbolic growth and decline are characterized by a sudden and complete breakout or breakdown that instantly reaches infinity. For example, a company with a high debt load based on floating rates may be marginally profitable at a 3% base rate, at 4% it may struggle but survive, at 5% it suddenly and dramatically fails.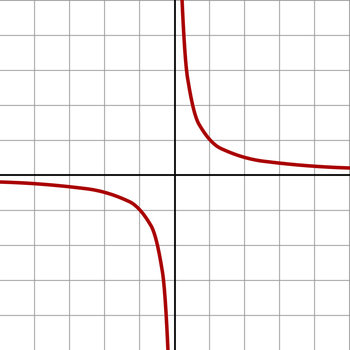
| Exponential vs Hyperbolic | ||
Exponential | Hyperbolic | |
Definition | Growth defined by an exponential function. | Growth that reaches a singularity at a finite point. |
Example Equation | y = 2x | y = 1/x |
Example Scenario | Economic growth, pollution | Technological singularity, things that fail at a point such as a bridge that fails at a certain load. |